Problem plecakowy
Dyskretny problem plecakowy (ang. discrete knapsack problem) jest jednym z najczęściej poruszanych problemów optymalizacyjnych.
Nazwa zagadnienia pochodzi od maksymalizacyjnego problemu wyboru
przedmiotów, tak by ich sumaryczna wartość była jak największa i
jednocześnie mieściły się w plecaku. Przy podanym zbiorze elementów o
podanej wadze i wartości, należy wybrać taki podzbiór by suma wartości
była możliwie jak największa, a suma wag była nie większa od danej
pojemności plecaka.
Problem plecakowy często przedstawia się jako problem złodzieja
rabującego sklep – znalazł on N towarów; j–ty przedmiot jest wart 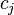 oraz waży
oraz waży  .
Złodziej dąży do zabrania ze sobą jak najwartościowszego łupu, przy
czym nie może zabrać więcej niż B kilogramów. Nie może też zabierać
ułamkowej części przedmiotów (byłoby to możliwe w ciągłym problemie
plecakowym).
.
Złodziej dąży do zabrania ze sobą jak najwartościowszego łupu, przy
czym nie może zabrać więcej niż B kilogramów. Nie może też zabierać
ułamkowej części przedmiotów (byłoby to możliwe w ciągłym problemie
plecakowym).
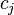 oraz waży
oraz waży  .
Złodziej dąży do zabrania ze sobą jak najwartościowszego łupu, przy
czym nie może zabrać więcej niż B kilogramów. Nie może też zabierać
ułamkowej części przedmiotów (byłoby to możliwe w ciągłym problemie
plecakowym).
.
Złodziej dąży do zabrania ze sobą jak najwartościowszego łupu, przy
czym nie może zabrać więcej niż B kilogramów. Nie może też zabierać
ułamkowej części przedmiotów (byłoby to możliwe w ciągłym problemie
plecakowym).
Podobny problem pojawia się często w kombinatoryce, teorii złożoności obliczeniowej, kryptografii oraz matematyce stosowanej.
Decyzyjna wersja przedstawionego zagadnienia to pytanie "czy wartość co najmniej C może być osiągnięta bez przekraczania wagi W?"
Definicja
Definicja formalna: mamy do dyspozycji plecak o maksymalnej pojemności  oraz zbiór
oraz zbiór  elementów
elementów  , przy czym każdy element ma określoną wartość
, przy czym każdy element ma określoną wartość 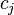 oraz wielkość
oraz wielkość  .
.
 oraz zbiór
oraz zbiór  elementów
elementów  , przy czym każdy element ma określoną wartość
, przy czym każdy element ma określoną wartość 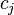 oraz wielkość
oraz wielkość  .
.
Dyskretny problem plecakowy (ang. 0-1 knapsack problem)
- formalnie problem może być zdefiniowany:
- zmaksymalizuj
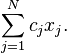
- przy założeniach:

Problem plecakowy, w którym liczba elementów danego typu jest ograniczona przez podaną wartość (ang. bounded knapsack problem).
- Formalnie:
- zmaksymalizuj
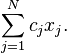
- przy założeniach:

Można rozważać także przypadek w którym nie ma wartości ograniczającej liczbę elementów danego typu (ang. unbounded knapsack problem).
W ciągłym problemie plecakowym można brać ułamkowe części przedmiotów.
W przypadku, gdy problem jest rozważany przy założeniach, że
- jest problemem decyzyjnym
- jest dyskretny
- dla każdego elementu waga równa się wartości

utożsamiany jest z problemem: czy dla danego zbioru liczb całkowitych
istnieje taki jego podzbiór, że suma jego liczb wynosi dokładnie W? Zagadnienie to nazywane jest problemem sumy podzbioru.
Problem plecakowy może być rozwiązany przy użyciu programowania dynamicznego, ale rozwiązanie wielomianowe nie jest znane. Problem plecakowy oraz sumy podzbioru są problemami NP trudnymi, co było powodem użycia sumy podzbioru jako podstawy w niektórych systemach kryptografii asymetrycznej takich jak Merkle-Hellman. Algorytmy takie używały grup,
nie liczb całkowitych. Merkle-Hellman oraz kilka podobnych algorytmów
zostało w późniejszym czasie złamanych, ponieważ szczególny problem sumy
podzbioru użyty w tych algorytmach były rozwiązywalne w czasie wielomianowym.
Decyzyjna wersja problemu plecakowego opisana wyżej jest problemem NP zupełnym i jest jednym z 21 NP zupełnych problemów Karpa.
Realizacje algorytmu
Przegląd zupełny
Przegląd zupełny (bruteforce, metoda siłowa) – metoda nieefektywna obliczeniowo (ale optymalna, gdyż znajduje rozwiązanie najlepsze); w jego przypadku złożoność obliczeniowa algorytmu wyniesie 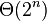 , co zdecydowanie zawyży czas działania dla dużych n. Złożoność wynosi
, co zdecydowanie zawyży czas działania dla dużych n. Złożoność wynosi 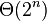 ponieważ jest tyle możliwych ciągów zero jedynkowych na n polach.
Złożoność można również obliczyć ze wzoru dwumianowego Newtona (dwumian Newtona) podstawiając za a i b jedynki.
ponieważ jest tyle możliwych ciągów zero jedynkowych na n polach.
Złożoność można również obliczyć ze wzoru dwumianowego Newtona (dwumian Newtona) podstawiając za a i b jedynki.
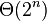 , co zdecydowanie zawyży czas działania dla dużych n. Złożoność wynosi
, co zdecydowanie zawyży czas działania dla dużych n. Złożoność wynosi 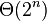 ponieważ jest tyle możliwych ciągów zero jedynkowych na n polach.
Złożoność można również obliczyć ze wzoru dwumianowego Newtona (dwumian Newtona) podstawiając za a i b jedynki.
ponieważ jest tyle możliwych ciągów zero jedynkowych na n polach.
Złożoność można również obliczyć ze wzoru dwumianowego Newtona (dwumian Newtona) podstawiając za a i b jedynki.











 zmienia się w niewielkim stopniu na przedziale
zmienia się w niewielkim stopniu na przedziale  , reguła taka da dobre przybliżenie całki.
, reguła taka da dobre przybliżenie całki.

 dzielimy przy tym na
dzielimy przy tym na  równych części o długościach:
równych części o długościach: .
.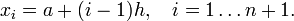
 – wartości funkcji w punktach podziału.
– wartości funkcji w punktach podziału.


![\mathbb{R} \supset [a,b] \ni x \mapsto f(x) \in \mathbb{R}](http://upload.wikimedia.org/math/f/9/a/f9a3a8b029499466aa4ca3d0f2f0f0e4.png)
![[a,b].](http://upload.wikimedia.org/math/d/5/f/d5f1c430bf683ed676382edef55aa192.png) A zatem znalezienie takiego
A zatem znalezienie takiego ![x^{\ast} \in [a,b],](http://upload.wikimedia.org/math/8/0/7/80730064af468f0077bd55ece001ac2f.png) które spełnia następujące równanie:
które spełnia następujące równanie:

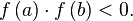



![m=\min_{x \in [a,b]} |f'(x)|](http://upload.wikimedia.org/math/2/3/f/23f5e45cf8e8e67f888246b722048093.png)
![M=\max_{x \in [a,b]} |f''(x)|](http://upload.wikimedia.org/math/e/0/6/e06ff2b483398a702e1414d12af29bb6.png)
 to przyjęta dokładność obliczeń):
to przyjęta dokładność obliczeń):

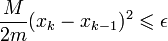
 Oznacza to, iż przy spełnionych założeniach błąd maleje kwadratowo wraz z ilością iteracji.
Oznacza to, iż przy spełnionych założeniach błąd maleje kwadratowo wraz z ilością iteracji.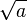 dla każdej liczby
dla każdej liczby 


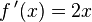
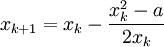

 i
i  algorytm przebiega następująco:
algorytm przebiega następująco:
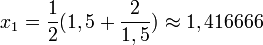
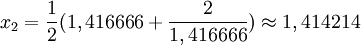

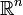 oraz
oraz  będzie funkcją
będzie funkcją 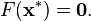
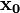 (często wybiera się wektor zerowy lub wektor jedynek), a następnie
rekurencyjnym przekształcaniu tego wektora aż do momentu gdy kolejne
przybliżenia będą satysfakcjonujące. Wektory przekształcane są zgodnie z
równaniem macierzowym:
(często wybiera się wektor zerowy lub wektor jedynek), a następnie
rekurencyjnym przekształcaniu tego wektora aż do momentu gdy kolejne
przybliżenia będą satysfakcjonujące. Wektory przekształcane są zgodnie z
równaniem macierzowym:
 jest pochodną (Frécheta) – jest to de facto macierz wielkości
jest pochodną (Frécheta) – jest to de facto macierz wielkości 
 efektywniej jest rozwiązać układ równań (tożsamy z powyższym równaniem):
efektywniej jest rozwiązać układ równań (tożsamy z powyższym równaniem):

 oraz dokładności
oraz dokładności 

 dla pewnego
dla pewnego 
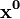 będącego dostatecznie blisko x*, wielowymiarowa metoda Newtona jest zbieżna oraz zbieżność ta jest kwadratowa.
będącego dostatecznie blisko x*, wielowymiarowa metoda Newtona jest zbieżna oraz zbieżność ta jest kwadratowa.
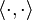 oznacza iloczyn skalarny dwóch wektorów.
oznacza iloczyn skalarny dwóch wektorów.