Wyszukiwanie lidera w zbiorze liczbowym

Wyszukiwanie lidera w zbiorze liczbowym 

Lider to taka wartość w zbiorze elementów, która powtarza się więcej niż razy. Jeśli istnieje taka wartość, to jest ona tylko jedna. Prześledźmy przykłady:
ciąg liczb

nie posiada lidera, ponieważ żadna z liczb nie wystąpiła co najmniej razy.

Ciąg

także nie posiada lidera, natomiast dla  liczb

liderem jest liczba .

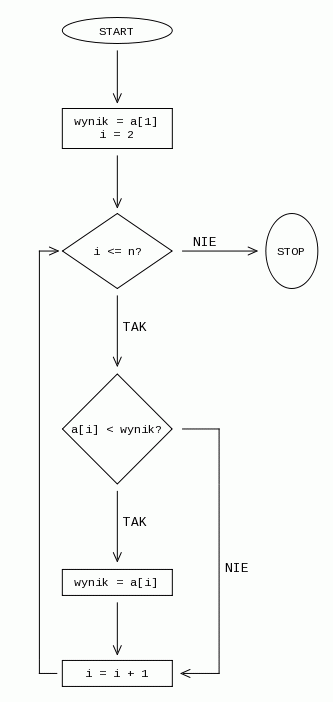
Strategia jest następująca. Przeszukujemy liniowo kolejne elementy i w danym etapie dwa różne elementy zbioru wykreślamy - tak jak by ich nie było. Jeśli lider występuje w zbiorze, to jego "pozycja" w otrzymanym podzbiorze się nie zmieni. Przeanalizujmy następujący przykład:

i pozostał na zbiór, w którym nadal mamy lidera:

Redukując w ten sposób elementy dochodzimy do sytuacji, gdy pozostanie element, który jest kandydatem na lidera. Musimy teraz tylko liniowo zliczyć i sprawdzić, czy dana wartość występuje więcej niż razy.

Warto podkreślić, że znaleziony element nie musi być liderem. Prześledźmy przykład, w którym nie ma lidera:

Po wykreśleniu dwóch początkowych wyrazów pozostaje podzbiór

,

w którym jest lider.

W programie przedstawionym poniżej ważną rolę odgrywa zmienna . Odpowiedzialna jest ona za kontrolowanie wykreślania dwóch elementów o różnych wartościach. Jeśli wykreślimy wszystkie elementy, oznacza to, że żadna wartość nie spełnia oczekiwań. Przeanalizujmy przypadek:

W przypadku znalezienia liczby różnej od aktualnego lidera, wykreślamy ją zmniejszając wartość zmiennej . Gdy znajdziemy taką samą, wartość zmiennej inkrementujemy. Jeśli  będzie liczbą większą od zera, oznacza to, że zmienna przechowuje potencjalnego lidera zbioru.

 

Sprawdzanie monotoniczności ciągu

Sprawdzanie monotoniczności ciągu 

 Ponieważ każdy ciąg jest funkcją, więc można dla nich też zdefiniować pojęcie monotoniczności w identyczny sposób. Otrzymujemy w ten sposób definicje ciągu stałego, ciągu rosnącego, ciągu malejącego, ciągu nierosnącego, ciągu niemalejącego, ciągu monotonicznego i ciągu ściśle monotonicznego. Intuicyjnie, wyrazy ciągu rosnącego ciągle się zwiększają, malejącego ciągle maleją.
Aby zbadać monotoniczność ciągu o danym wyrazie ogólnym, należy zbadać znak różnicy a_n+1 - a_n. Jeśli jest ona dodatnia wtedy ciąg jest rosnący, jeśli ujemna ciąg jest malejący, a jeśli równa 0, to ciąg jest stały.

Szukanie maksymalnego i minimalnego elementu ciągu

Szukanie maksymalnego i minimalnego elementu ciągu 

 Załóżmy że mamy daną tablicę n-elementów i chcemy odnaleźć w niej element minimalny (bądź maksymalny). Niech będzie to tablica a o indeksach od 1 do n. Czyli kolejne jej elementy oznaczymy: a[1], a[2], a[3], ..., a[n-1], a[n].

By odnaleźć element minimalny podejmiemy następujące kroki:

• na początku zainicjujemy wynik pierwszą wartością z tablicy, czyli a[1],
• następnie przejdziemy po kolejnych elementach tablicy (rozpoczynając od drugiego) i jeżeli dany element tablicy jest mniejszy od naszego wyniku, to zaktualizujemy nasz wynik przypisując do niego ten element,
• po przejściu po wszystkich elementach otrzymamy w wyniku element najmniejszy w tablicy.

Operację odnajdowania minimalnego elementu w tablicy możemy zapisać następującym schematem blokowym:

 

Poszukiwanie ciągu liczbowego z wartownikiem

Poszukiwanie ciągu liczbowego z wartownikiem

Załóżmy że mamy daną tablicę n-elementów i chcemy odnaleźć w niej zadany element x. Niech będzie to tablica a o indeksach od 1 do n. Czyli kolejne jej elementy oznaczymy: a[1], a[2], a[3], ..., a[n-1], a[n].
Jeżeli przyjrzymy się dokładnie klasycznemu algorytmowi przeglądania tablicy w poszukiwaniu elementu:

 

zauważymy, że dla każdego elementu wykonywane są dwa porównania:

• pierwsze: czy znaleźliśmy się już na końcu tablicy,
• drugie: czy aktualnie przeglądany element jest równy poszukiwanemu.

Liczbę porównań można zredukować wykorzystując algorytm wyszukiwania z wartownikiem. Nazwa tego algorytmu bierze się ze sposobu, w jaki wykorzystywany jest element szukany x.

By odnaleźć element x podejmiemy następujące kroki:

• na końcu tablicy (czyli pod indeksem n+1) wstawimy szukany element x - będzie to nasz wartownik, w przypadku gdy nie znajdziemy go nigdzie indziej w tablicy, zabezpieczy nas on przed wyjściem poza tablicę,
• przejdziemy po kolejnych elementach tablicy, tak długo aż nie znajdziemy szukanego elementu,
• w momencie znalezienia szukanego elementu x sprawdzamy, który jest to element tablicy? Jeżeli jest to ostatni element tablicy (n+1) to trafiliśmy na naszego wartownika i oznacza to, że w tablicy nie było szukanego elementu x, w przeciwnym razie element x został odnaleziony.

W stosunku do klasycznego algorytmu wyszukiwania oszczędzamy czas na sprawdzaniu czy osiągnęliśmy koniec tablicy. Sprawdzenie to występuje raz - po odnalezieniu elementu szukanego, a nie tak jak poprzednio przed każdym sprawdzeniem kolejnego elementu.

Algorytm ten mimo, że jest szybszy od zwykłego wyszukiwania to ma taką samą jak on złożoność obliczeniową wynoszącą O(n), co oznacza, że czas potrzebny na wyszukanie elementu tą metodą rośnie w sposób liniowy wraz z liniowym wzrostem liczby elementów w przeszukiwanej tablicy. To znaczy, że czas potrzebny na wyszukanie dwa razy większej liczby elementów wzrośnie dwukrotnie.
Podczas implementowania tego rozwiązania należy zapewnić miejsce w tablicy potrzebne do dodania wartownika. Należy więc deklarować tablicę o rozmiarze o jeden większym jak liczba przechowywanych elementów.

Poszukiwanie ciągu liczbowego

Poszukiwanie ciągu liczbowego

Algorytmy przeszukiwania

---

Szukanie elementu

Często spotykanym rodzajem przeszukiwania jest wyszukiwanie elementu posiadającego pewną szczególną własność, jak np. najmniejszy, największy, podzielny przez jedenaście - element taki możemy nazwać idealnym.
Algorytm znajdowania elementu idealnego polega na wstępnym przyjęciu, że elementem idealnym jest pierwszy z dostępnych, a następnie na porównywaniu kolejnych elementów z elementem dotychczas uznanym za idealny. Jeśli podczas porównania okaże się, że element porównywany jest bliższy ideałowi niż dotychczasowy ideał, to wykonuje się zamianę przyjmując za ideał element aktualnie porównywany.
Poniższy fragment kodu znajduje w ciągu liczb podawanych przez użytkownikaliczbę największą:

Write('Podaj pierwsza liczbę ciągu = ');
ReadLn(Maksymalny);
For I:=2 To N Do
  Begin
    Write('Kolejna liczba = ');
    ReadLn(Liczba);
    If Liczba>Maksymalny Then Maksymalny:=Liczba;
  End;

Niżej przykłady programów szukających: podzielne, podzielne2, Ile_razy, liczby pierwsze.

---

Przeszukiwanie binarne

Przeszukiwanie binarne jest algorytmem sprawdzającym czy uporządkowany rosnąco ciąg liczbowy N-elementowy zawiera szukaną liczbę x (nazywane jest też przeszukiwaniem połówkowym).
Algorytm przeszukiwania binarego wykorzystuje uporządkowanie ciągu liczbowego dzieląc go każdorazowo na połowy. Poszukiwaną liczbę x porównuje się z liczbą środkową ciągu i w zależności od wyniku tego porównania przeszukiwana jest albo lewa, albo prawa część tablicy. Obszar poszukiwania wyznaczają dwa indeksy: start i stop. oznaczają one odpowiednio początek i koniec przeszukiwanego fragmentu tablicy - rozpoczynając przeszukiwanie zmiennym tym przypisujemy wartości start:=1 i stop:=N, zakończenie przeszukiwania następuje gdy przeszukiwany fragment tablicy zmaleje do jednego elementu, to znaczy, gdy start=stop.

  DANE:
     a - przeszukiwana tablica (posortowana rosnąco)
     x - poszukiwana liczba
     N - rozmiar tablicy
  WYNIK:
  prawda, jeżeli tablica "a" zawiera liczbę "x"

1. Przyjmij: start:=1; stop:=N;
2. Dopóki start<stop;
   • Wyznacz środek przedziału sr=(start+stop) Div 2,
   • Jeżeli poszukiwana liczba x jest nie większa niż liczba w środku tablicy, to odrzuć prawą jej część przyjmując za stop:=sr;
   • W przeciwnym wypadku odrzuć część lewą przyjmując za start:=sr+1;
3. Teraz start=stop, zwróć prawdę jeśli a[start]=x.

Oto rekurencyjna funkcja szukająca:

  Type Tablica = Array[1..1000] Of Integer;

  Function Szukaj(Var a: Tablica; x, n : Integer) : Boolean;
    Var start, stop, sr : Integer;
  Begin
    start:=1;
    stop:=n;
    While start<stop Do
      Begin
        sr:=(start+stop) Div 2;
        If x<=a[sr] Then stop:=sr Else start:=sr+1;
      End;
    Szukaj:=(a[start]=x);
  End;

Sito Eratostenesa

Sito Eratostenesa

Sito Eratostenesa - przypisywany Eratostenesowi z Cyreny algorytm wyznaczania liczb pierwszych z zadanego przedziału .

Algorytm

 

Ze zbioru liczb naturalnych z przedziału , tj. , wybieramy najmniejszą, czyli 2, i wykreślamy wszystkie jej wielokrotności większe od niej samej, to jest .

	2	3	-4-	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	-44-	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60

Z pozostałych liczb wybieramy najmniejszą niewykreśloną liczbę (3) i usuwamy wszystkie jej wielokrotności większe od niej samej: , przy czym nie przejmujemy się tym, że niektóre liczby (na przykład 6 czy 12) będą skreślane więcej niż raz.

	2	3	-4-	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	-44-	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60

Według tej samej procedury postępujemy dla liczby 5.

	2	3	-4-	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	-44-	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60

Następnie dla 7, 11, 13; aż do sprawdzenia wszystkich niewykreślonych wcześniej liczb.

	2	3	-4-	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	-44-	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60

Wykreślanie powtarzamy do momentu, gdy liczba , której wielokrotność wykreślamy, będzie większa niż .
Dla danej liczby wszystkie niewykreślone liczby mniejsze, bądź równe są liczbami pierwszymi.

	2	3	-4-	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	-44-	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60

Sprawdzanie czy liczba jest liczbą pierwszą

***LICZBY PIERWSZE- KLIK

Sprawdzanie czy liczba jest liczbą pierwszą

 

Zacznijmy od definicji liczby pierwszej. Liczba pierwsza to taka liczba naturalna większa od 1, która dzieli się tylko przez 1 i samą siebie. Oto kilka liczb pierwszych:

Warto zauważyć, że takich liczb jest nieskończenie wiele.

Aby określić, czy dana liczba jest pierwsza należy zbadać jej dzielniki. Dla zadanej liczby n sprawdzamy kolejne liczby naturalne należące do przedziału:

Jeśli któraś z tych liczb jest dzielnikiem, oznacza to, że nasza liczba nie jest pierwsza.

 

Zmienopozycyjna reprezentacja liczb

Zmienopozycyjna reprezentacja liczb

• Reprezentacja zmiennopozycyjna charakteryzuje się zmiennym położeniem kropki dziesiętnej.
  Przykład
  

  602252000000000000000000*101		wartość liczby jest w każdym przypadku taka sama, zmienia się tylko położenie kropki dziesiętnej
  6,02252*1023
  0,602252*1024
  602252*1022

  
  
• W podobny sposób przedstawiane są liczby w formacie naukowym w arkuszu kalkulacyjnym: 4,92e³⁶, czyli 4,92*10⁺³⁶
• Aby liczby zapisane w ten sposób można było porównywać ze sobą, stosuje się znormalizowaną reprezentację zmiennopozycyjną, gdzie liczba przedstawiona jest jako iloczyn
  a=m*10^c
  m - mantysa,  0,1<=|m|<1
  c - cecha, liczba całkowita
  Przykład: 0,662607*10^-33

 

Stałopozycyjna reprezentacja liczb

Stałopozycyjna reprezentacja liczb

• Reprezentacja stałopozycyjna charakteryzuje się stałym położeniem kropki dziesiętnej.
• Na część całkowitą liczby oraz na część ułamkową przeznaczona jest stała, z góry określona liczba bitów.
• Jeśli na część ułamkową przeznaczone jest 0 bitów to reprezentacja stałopozycyjna służy do przechowywania liczb całkowitych.
• Jeśli liczba, którą chcemy przedstawić w tej reprezentacji, mieści się na ustalonej liczbie bitów, to może być reprezentowana dokładnie.
• Jeśli wynik działań wykonywanych na liczbach stałopozycyjnych nie mieści się na ustalonej liczbie bitów, powstaje nadmiar w obliczeniach (wynik jest błędnie interpretowany przez komputer).
• Mając do dyspozycji n bitów możemy w reprezentacji stałopozycyjnej przedstawić liczby całkowite z zakresu:
  -2^n-1 .. 2^n-1-1
  
  Przykład
   
• n=8:    -2⁷ .. 2⁷-1, czyli -128 .. 127, odpowiada to typowi danych ShortInt (C++: char)
  n=16:   -2¹⁵ .. 2¹⁵-1, czyli -32788 .. 32787, odpowiada to typowi danych Integer (C++: short)
  n=32:   -2³¹ .. 2³¹-1, czyli -2 147 483 648 .. 2 147 483 647, odpowiada to typowi danych LongInt (C++: int)
   
• Deklaracja odpowiedniego typu zmiennych w programie określa dopuszczalny zakres danych.

Liczby PIERWSZE - 14.02.2014

Liczby pierwsze

Zagadnienie odróżniania liczb pierwszych od złożonych i rozkładanie tych ostatnich na czynniki pierwsze uchodzi za najważniejsze i o dużym praktycznym znaczeniu w arytmetyce. Carl Friedrich Gauss
Iloczyn liczb naturalnych jest zawsze liczbą naturalną, są więc liczby naturalne, będące iloczynami dwóch liczb naturalnych większych od jedności. Są także liczby naturalne większe od jedności, które nie są iloczynami dwóch liczb naturalnych większych od jedności. Takie właśnie liczby nazywamy pierwszymi. Liczby pierwsze to swego rodzaju cegiełki służące do budowania kolejnych liczb naturalnych.
Liczby pierwsze to liczby naturalne, które posiadają dokładnie dwa dzielniki (liczbę 1 i samą siebie).
Oto kilka początkowych liczb pierwszych: 2, 3, 5, 7, 11, 13, 17, 19 ...
Nasuwa się pytanie, czy liczba naturalna jest pierwsza, czy też nie jest liczbą pierwszą. Jeśli liczba naturalna większa od 1 nie jest pierwszą, to jest iloczynem dwóch liczb naturalnych od niej mniejszych. Liczby takie nazywamy liczbami złożonymi.
Liczby złożone to liczby naturalne, które posiadają więcej niż dwa dzielniki.
Przykłady liczb złożonych: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, ...
Liczby 0 i 1 nie należą ani do liczb pierwszych ani do złożonych. Kiedyś uznawano liczbę 1 za pierwszą, jest ona jednak tak różna od właściwych liczb pierwszych, że dziś lokuje się ją w odrębnej klasie, nosi nazwę jedności.

SYSTEMY LICZBOWE

Systemy liczbowe

   Wstęp

   Art ten jest dla tych wszystkich, którzy mają problemy ze zrozumieniem systemów liczbowych. Dodam jeszcze od siebie, że żaden haker, programista czy "chociażby" informatyk, nie zajedzie daleko bez niniejszej wiedzy. Powiem nawet więcej: jest to podstawa dobrego komputerowca. Bez tego nie masz co się uczyć języków programowania. Nie jest to zwykły kurs tejże wiedzy. Nie będę tu, bowiem stosował żadnych oznaczeń. Nie, dlatego, że mi się nie chcę, ale żeby było wam łatwiej wszystko zrozumieć. Zastąpię je obszernymi opisami. Skoro wszystko już jest jasne, można zaczynać. 


   System dziesiętny

   Dla nas, ludzi naturalnym sposobem prezentacji liczb jest system dziesiętny. Oznacza to, że wyróżniamy dziesięć cytr. Są nimi: zero, jeden, dwa, trzy, cztery, pięć, sześć, siedem, osiem oraz dziewięć. Oznacza się je odpowiednio: 0, 1, 2, 3, 4, 5, 6, 7, 8 oraz 9. Jak widać, wliczając zero, jest ich dziesięć. Spróbujcie uświadomić sobie, że liczenie jest tylko i wyłącznie ILOŚCIĄ, a nie zapisem liczb. Zapis dziesiętny powstał wieki temu, prawdopodobnie, dlatego, że mamy dziesięć palców. Jednakże, nie będziemy teraz się zajmować historią.

   Przejdźmy zatem do bardziej konkretnych rzeczy. Umiemy już policzyć do dziecięciu, wliczając liczbę zero. Natomiast co się stanie, gdy będziemy mieli do policzenia jakąś większą ilość? Otóż, przeskakujemy automatycznie, na następną pozycję, a cyfry zwiększmy tylko na pozycji wysuniętej najbardziej w prawo. Właśnie ta najbardziej w prawo wysunięta pozycja jest najsłabsza, a najbardziej w lewo - najmocniejsza. Tym sposobem znowu zwiększamy cyfry, aż uzyskamy dziewięć. Następna liczba, przesunie cyfrę, która znajduje się o jedną pozycję w lewo. Natomiast gdy już nawet dziewiątka będzie na najbardziej w lewo wysuniętej pozycji, dodajemy nową pozycję. Cykl zaczyna się ponownie i tak w nieskończoność. Może wydać się wam to trochę skomplikowane, ale sobie to wyjaśnimy na przykładzie. Weźmy na przykład liczbę 274, czyli dwieście siedemdziesiąt cztery. Na najsłabszej pozycji widnieje cyfra 4. Pozycja ta nosi nazwę pozycji jedności, jeśli pamiętacie ze szkoły podstawowej. Mamy zatem 4 jedności. Na drugiej pozycji jest cyfra 7. Cyfra ta znajduje się na drugiej pozycji, czyli pozycji dziesiątek. Można więc powiedzieć, że jest tam siedem dziesiątek, inaczej mówiąc 70 jedności. Na trzeciej natomiast pozycji jest cyfra 2. Trzecia pozycja to pozycja setek, czyli mam dwie setki. Innymi słowy, liczba 274 to dwie setki, siedem dziesiątek i 4 jedności. Można to zapisać następująco: 4*1 + 7*10 + 2*100. Po dokonaniu tegoż działania, wyjdzie 274. Czas, aby się temu działaniu przyjrzeć. Jak widać, każdy kolejny składnik zawiera cyfrę z powyższej liczby oraz ciągle zwiększający mnożnik. Mnożnik ten najpierw jest równy 1, potem 10, a na końcu 100. Znaczy to, że każdy następny jest pomnożony przez 10. Można więc zapisać to jeszcze inaczej. Liczba 274 to tak jak: 4*10⁰ + 7*10¹ + 2*10². Jak widzimy, mnożnik to liczba 10 z ciągle zwiększającą się potęgą. 

   Ta informacja przyda się w następnych działach omawiających przeliczanie z jednego systemu na drugi. Zwróćmy uwagę teraz na rzecz, która chociaż trochę uzmysłowi wam, jak działa system dziesiętny. Gdybyśmy chcieli zwiększyć o 1 liczbę 347, to zawsze, automatycznie zwiększmy cyfrę, która znajduję się na pozycji wysuniętej najdalej w prawo. Powstanie zatem 348. Natomiast, gdy chcemy zwiększyć o 1 liczbę 429, widzimy, że nie można już nic do 9-tki dodać, gdyż nie ma już wyższej cyfry. Co wtedy robimy? - każdy wie. Zwiększamy o jeden wartość cyfry znajdującej się na pozycji z lewej strony,  natomiast wartość jedności zerujemy (dajemy najniższą możliwą wartość). Powstaje zatem 430. Jezeli natomiast chcielibyśmy zwiększyć wartość o 1 liczby 999, to widać, że : nie można zwiększyć jedności, nie można zwiększyć dziesiątek i nie można zwiększyć setek. Dodajemy zatem następną pozycję. Powstanie więc 1000. 

   Mam nadzieję, że w powyższym akapicie wyjaśniłem wam jak działa ten przeklęty system dziesiętny i możemy już przystąpić do bardziej spektakularnych operacji. Jeśli nie zrozumiałeś nic z powyższego tekstu, wracaj do początku i zacznij jeszcze raz, gdyż nic tu po tobie. Natomiast, w sytuacji, gdy wszystko rozumiesz - zapraszam do następnego akapitu. 


   System ósemkowy

   Skoro powstał system dziesiętny, można wymyślać dowolne systemy liczenia (na przykład czwórkowy itd.). Właśnie jednym z takich systemów jest system ósemkowy. Początkowo był on trochę stosowany, obecnie jednak jego zastosowanie jest znikome. Posłuży nam on jako dobry przykład. Jak się pewnie domyślacie, w systemie tym jest osiem cyfr. Wcale się nie mylicie. Są to: 0, 1, 2, 3, 4, 5, 6 oraz 7. Jest ich, więc 8, stąd nazwa. Działa on na tej samej zasadzie, co system dziesiętny. To znaczy, że gdy już jakaś cyfra jest na maksymalnej wartości, zwiększamy cyfrę na następnej pozycji. Wyjaśni to się na przykładzie. Przekształcajmy kolejne liczby i zobaczmy, jakie są różnice. Liczba zero (0) tak samo wygląda w obu systemach. Tak samo ma się sytuacja z jedynką (1), dwójką (2), trójką (3) itd. Sytuacja staje się skomplikowana, gdy dojedziemy do siódemki (7). Liczba 7 wygląda tak samo w obu systemach. Jednak nadchodzi następna liczba, zwana przez nas jako osiem. System ósemkowy nie zna takiej cyfry, więc powstaje następna pozycja. Zatem liczba osiem (8) w systemie dziesiętnym to liczba dziesięć (10) w systemie ósemkowym. Była to bardzo ważna konwersja i dobrze by było, gdybyś ją zrozumiał. Liczby takie jak: 6, 7, 8, 9, 10, w systemie ósemkowym będą wyglądać odpowiednio: 6, 7, 10, 11, 12. 

   Gdybyśmy chcieli sprawdzić, czy rzeczywiście liczba na przykład 14 w systemie ósemkowym to 12 w dziesiętnym, musimy przeprowadzić konwersję. Dokonuje tego tak, jak robiliśmy to w akapicie o systemie dziesiętnym, z tym, że podstawą mnożenia będzie liczba 8. Zatem, rozpisujemy liczbę 14 (s. ósemkowy) w następujący sposób. Jest to 4*1 + 1*8, czyli 4+8 czyli 12. Innymi słowy, jest to 4*8⁰ + 1*8¹. Po policzeniu wyniku muszą się zgadzać. 

   Zauważcie, że w systemie dziesiętnym kolejne pozycje miały wartości: 1, 10, 100, 1000, 100000, 1000000 itd., ponieważ podstawą była liczba 10. W systemie ósemkowym podstawą jest liczba 8, a kolejne pozycje wyglądają następująco: 1, 8, 64, 512, 4096, 32768 itd. 


   System dwójkowy czyli binarny

   Powiedzieliśmy sobie, że można wymyślać dowolny system zapisu liczb. Skoro tak, to, czemu miałby nie powstać system dwójkowy, składający się tylko z dwóch cyfr: 0 (zero) i 1 (jeden). Działa on analogicznie tak samo jak poprzednie systemy. Wyjaśni się zaraz wszystko na konkretnym przykładzie. Weźmy na przykład kilka pierwszych liczb naszego systemu dziesiętnego. Będziemy je konwertować na system dwójkowy, zwany również binarnym. Pierwsza liczba w naszym systemie to 0 (zero). W systemie dwójkowym, liczba ta również jest równa 0, gdyż istnieje tam taka cyfra. Kolejna liczba to 1 (jeden). W systemie dwójkowym, również taka cyfra istnieje, więc zapisujemy 1. Kolejna liczba to 2 (dwa). Wiemy, że nie istnieje tam taka cyfra, więc dodajemy kolejną pozycję, a pozycję wysuniętą na prawo, zerujemy. Zatem liczba 2 w systemie dziesiętnym ma postać "10" w systemie dwójkowym. Bynajmniej nie jest to "dziesięć" tylko "jeden, zero". Kolejne liczby w systemie dziesiętnym to: 3, 4, 5, 6, 7, 8, 9 itd. W systemie dwójkowym wyglądają one odpowiednio: 11, 100, 101, 110, 111, 1000, 1001. Jak widzimy, zasada jest cały czas taka sama.

   Zanim zaczniemy uczyć się, jak w prosty sposób zamienić liczbę z jednego systemu na drugi, postawmy sobie pytanie: Po co komputerowi taki system? 

   No więc, jak zapewne wszyscy wiedzą, komputer składa się z części elektronicznych. Wymiana informacji polega na odpowiednim przesyłaniem sygnałów. Podstawą elektroniki jest prąd elektryczny, który w układach elektronicznych albo płynie albo nie. Zatem, aby łatwiej było komputerowi rozpoznawać sygnały, interpretuje on płynący prąd jako "1" (jeden), a jego brak jako "0" (zero). Nie trudno się domyślić, że komputer operując odpowiednim ustawieniem, kiedy ma płynąc prąd, a kiedy nie ustawia różne wartości zer i jedynek. Procesor konwertuje je na liczby i w ten sposób powstają czytelne dla nas obrazy, teksty, dźwięk itd. Mam nadzieję, że w ten "chłopski" sposób wyjaśniłem wam mniej więcej jak to się odbywa. Nie tylko w postaci sygnałów elektrycznych reprezentowane mogą być zera lub jedynki. Również na wszelkich nośnikach, np. płyta CD, na której nagrywarka wypala malutkie wgłębienia. Właśnie te wgłębienia są jedynkami, a "równiny" zerami (albo i odwrotnie). 

   Zatem podsumujmy: komputer zna tylko zera i jedynki. Bity przyjmują tylko jedną z tych dwóch wartości. Osiem bitów to jeden bajt. Ustawienie ośmiu bitów decyduje o numerze, który może przyjąć maksymalnie 256. Numer decyduje o znaku, jaki komputer ma wykorzystać. 


   Konwersja liczby dwójkowej (binarnej) na dziesiętną

   Skoro już wiesz, po co nam system binarny, dowiesz się jak przeliczać go na nasz system dziesiętny. Otóż nie jest to zbyt skomplikowane. Przypomnijcie sobie sposób z liczbami w systemie ósemkowym. Tu oczywiście robimy to analogicznie tak samo, z tym, że podstawą jest naturalnie liczba 2. Weźmy sobie zatem jakąś liczbę zapisaną w systemie dwójkowym, np. 1000011. Jak już wcześniej mówiliśmy, zaczynamy od cyfr najsłabszych, czyli wysuniętych najbardziej na prawo. Najbardziej na prawo wysunięta jest cyfra 1, a więc tak jak poprzednio mnożymy ją przez podstawę systemu z odpowiednią potęgą. Podstawą systemu jest 2. Zatem, cała konwersja ma postać: 1*2⁰ + 1*2¹ + 0*2² + 0*2³ +0*2⁴ + 0*2⁵ +1*2⁶, a to się równa: 1 + 2 + 0 + 0 + 0 + 0 + 64, czyli jest to 67 w systemie dziesiętnym. Moje gratulację - udało się skonwertować liczbę w zapisie dwójkowym na zapis dziesiętny. Teraz dobrze by było gdybyś przeanalizował sobie dokładnie powyższą konwersję. Jeżeli jej nie rozumiesz - przeczytaj jeszcze raz. Jeżeli rozumiesz - zapraszam dalej. 


   Konwersja liczby dziesiętnej na dwójkową (binarną)

   Teraz, skoro już umiesz konwertować liczby z zapisu dwójkowego na dziesiętny warto by było skonwertować je odwrotnie, to znaczy z zapisu dziesiętnego na dwójkowy. Gdybyśmy liczyli na piechotę, byśmy musieli sprawdzać kolejne wielokrotności liczby 2. Sposób ten raczej jest mało stosowany, zajmijmy się trochę lepszym. Jest to prosty sposób, wcale nie wymaga myślenia. Najpierw bierzemy liczbę, jaką chcemy skonwertować na zapis dwójkowy. Weźmy liczbę z poprzedniego rozdziału i sprawdźmy, czy nam się to zgadza. Zatem, liczba którą będziemy konwertować to 67. Sposób jest następujący: liczbę dzielimy przez 2 i jeżeli wynik będzie z resztą: zapisujemy 1, jeżeli nie - zapisujemy 0. Następnie znowu dzielimy przez 2 to co zostało z liczby, ale bez reszty. Taki proces trwa, aż zostanie 0 (zero). Otrzymane zera i jedynki zapisujemy w odwrotnej kolejności. Wyjaśni się to wszystko na konkretnym przykładzie. Zatem do dzieła: 

67	:2 |	1
33	:2 |	1
16	:2 |	0
8	:2 |	0
4	:2 |	0
2	:2 |	0
1	:2 |	1

   Co daje 1000011. Jak widzimy, wynik zgadza się. Widać również, że zawsze na samym końcu po podzieleniu będzie 0, zatem ostatnia liczba jest równa 1. Jeden podzielić na dwa zawsze wyjdzie 0,5 zatem wynik z resztą. Co za tym idzie - pierwsza cyfra w zapisie dwójkowym jest ZAWSZE RÓWNA 1. Nie tylko matematycznie można to udowodnić. W elektronice, również musi być taka postać rzeczy. Przyjęliśmy bowiem, że dla komputera brak przepływu prądu oznacza "0", natomiast przepływ prądu - "1". Sygnał zatem nie może zaczynać się od "0", gdyż jest to brak sygnału. Procesor nie wie, czy sygnał już się zaczął, czy jeszcze nie. Początek musi być "1" (jest sygnał).


   System szesnastkowy czyli heksadecymalny

   Póki co znasz już 3 systemy liczbowe: dziesiętny, ósemkowy i dwójkowy. Wszystkie one działają analogicznie tak samo, zmienia się tylko podstawa, czyli ilość cyfr. Teraz zajmiemy się nieco systemem szesnastkowym inaczej zwanym heksadecymalnym. Jest on dość szeroko stosowany w dzisiejszej informatyce, zatem należało by go rozumieć. Jak się zapewne domyślasz, podstawą tego systemu jest 16. Musi istnieć więc szesnaście cyfr. Pierwsze dziesięć już znasz. Są nimi odpowiednio: 0, 1, 2, 3, 4, 5, 6, 7, 8 oraz 9. W naszym systemie, kolejną liczbą jest 10, natomiast w systemie szesnastkowym jest ono reprezentowane przez A. Kolejne liczby to: 11 - B, 12 - C, 13 - D, 14 - E, 15 - F. Zatem, np. liczby w systemie dziesiętnym: 2, 6, 9, 11, 14, w systemie szesnastkowym wyglądają odpowiednio: 2, 6, 9, B, E. Widać od razu, że duże liczby zajmują w systemie szesnastkowym mało miejsca. Dlatego właśnie jest on tak przydatny.


   Konwersja liczby szesnastkowej na dziesiętną

   Konwersja ta odbywa się podobnie jak w przypadku liczb binarnych, z tym, że podstawą jest nie 2 a 16. Weźmy dowolnie wymyśloną liczbę w zapisie szesnastkowym, na przykład AB12 (co czytamy: a b jeden dwa). Bierzemy cyfrę wysuniętą najbardziej w prawo i postępujemy tak samo jak w przypadku liczb dwójkowych, ale zamiast mnożnika 2 mamy 16. Zatem jest to: 2*16⁰ + 1*16¹ + 11*16² + 10*16³ , a więc jest to 2 + 16 + 2816 + 40960, a więc jest to liczba 43794 w zapisie dziesiętnym. 


   Konwersja liczby dziesiętnej na szesnastkowy

   No to warto by było teraz z powrotem odwrócić liczbę 43794 w zapisie dziesiętnym na AB12 w szesnastkowym. Jeżeli wiemy jak to się robi - nie ma problemu. Zatem zaczynajmy.

   Najpierw musimy sobie napisać jakie są kolejne wielokrotności liczby 16. A są to: 1, 16, 256, 4096, 65536 itd. Jak widać nasza liczba w systemie dziesiętnym, czyli 43794 jest między liczbą 4096, a 65536. Bierzemy pod uwagę liczbę mniejszą od naszej, czyli 4096. Jest ona czwartą wielokrotnością, więc nasza liczba w systemie szesnastkowym będzie miała 4 cyfry (na razie wszystko się zgadza). Teraz sprawdzam, ile razy liczba 4096 mieści się w naszej liczbie konwertowanej, czyli 43794. Okazuje się, że mieści się 10 razy. 10 w systemie szesnastkowym to A, zatem pierwsza cyfra to A. Jak widać, w dalszym ciągu wszystko się zgadza. Teraz, skoro liczba 4096 zmieściła się dziesięć razy w 43794, to jeszcze zapewne została jakaś reszta. Obliczamy sobie tą resztę. Mnożymy zatem 4096*10 co daje 40960. Teraz odejmujemy wynik od naszej liczby i obliczamy resztę. Zatem 43794 - 40960 = 2834. To jest nasza reszta. Następnie z resztą postępujemy tak samo, jak na początku konwersji. Już na oko widać, że w następnym kroku sprawdzamy ile razy 256 mieści się w 2834. Mieści się 11 razy, zatem kolejna cyfra szukanego zapisu to B. Następnie znowu: obliczamy resztę, itd. Końcowy wynik powinien wynosić AB12. Tak oto skonwertowaliśmy liczbę z zapisu dziesiętnego na szesnastkowy.


   Konwersja liczby dwójkowej na szesnastkowy

   I wydawać się może, że wkraczamy w coraz to bardziej zaawansowane progi – ale od razu mówię, że nie. Konwersja ta jest bardzo prosta i wcale nie wymaga skomplikowanych obliczeń. Najpierw zróbmy małą sztuczkę. Zobaczcie, jaka jest maksymalna liczba w zapisie dwójkowym składająca się z 4 bitów. Jeżeli liczba ma być maksymalna, wszystkie jej cyfry muszą mieć maksymalne wartości. Ma ona zatem postać: 1111. Po przeliczeniu, otrzymamy 15 w zapisie dziesiętnym. Jak pewnie zauważyliście, 15 jest to maksymalna cyfra w zapisie szesnastkowym, czyli F. Daje to trochę do myślenia, ale najważniejszy jest jeden fakt: każda liczba składająca się z czterech cyfr w zapisie dwójkowym da się zapisać jako jedna cyfra w zapisie szesnastkowym. Może to zabrzmiało groźnie, ale niedługo powinno się wytłumaczyć. Zatem, kolejne liczby w zapisie dwójkowym i szesnastkowym to: 

Zapis dwójkowy:	Zapis szesnastkowy:
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

   Weźmy dla przykładu wcześniej już wspomnianą liczbę 67 w systemie dziesiętnym. Przekształciliśmy ją na 1000011 w zapisie dwójkowym. Jak teraz z tego otrzymać zapis szesnastkowy? Otóż bardzo prosto. Dzielimy kod binarny na czterocyfrowe grupy od prawej strony zaczynając. Jeżeli z lewej strony nie będzie czterech cyfr - dopisujemy z przodu zera. Zatem, otrzymamy dwie grupy. Są to: 0100 oraz 0011. Teraz wystarczy zamienić je na odpowiednie cyfry z zapisu szesnastkowego (można się posłużyć powyższą tabelą). W efekcie otrzymamy: 43 w zapisie szesnastkowym. Warto by było jeszcze sprawdzić czy wynik się zgadza konwertując zapis szesnastkowy na dziesiętny. Zatem jest to: 3*16⁰ + 4*16¹, czyli 3 + 64, czyli 67 w zapisie dziesiętnym. Jak widzimy, wszystko się zgadza. 


   Konwersja liczby szesnastkowej na dwójkową

   A wykonuje ją się odwrotnie jak dwójkową na szesnastkową. Po prostu kolejne cyfry w zapisie szesnastkowym zapisujesz jako cztery cyfry w zapisie dwójkowym. Pamiętaj, że każda cyfra w zapisie szesnastkowym odpowiada jako 4 cyfry w zapisie dwójkowym (nie więcej i nie mniej). Ewentualnie możesz pozbyć się zer znajdujących się na najbardziej w lewo wysuniętej pozycji, aż znajdziesz tam jedynkę, gdyż mówiliśmy o tym, że kod binarny zawsze zaczyna się od 1 (np. jeśli wyjdzie 0001100101110 to możesz to zapisać jako 1100101110 pozbywając się zer z początku). 


 

<źródło: http://www.programuj.com/artykuly/rozne/sysliczb.php >